Solution:
Given the logarithmic function:
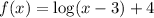
Domain:
The domain of the function is the set of input values for which the function is real and defined.
From f(x) function:
![f(x)=\operatorname{\log}(x-3)+4]()
The domain of the function is
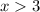
x-intercept:
The x-intercept of the function is the value of x for which the function f(x) equates to zero.
Thus,
![\begin{gathered} f(x)=\operatorname{\log}(x-3)+4 \\ where\text{ f\lparen x\rparen=0} \\ \Rightarrow\operatorname{\log}(x-3)+4=0 \\ subtract\text{ 4 from both sides of the equation} \\ \operatorname{\log}(x-3)+4-4=0-4 \\ \Rightarrow\operatorname{\log}(x-3)=-4 \\ take\text{ the antilogarithm of both sides,} \\ 10^{\operatorname{\log}(x-3)}=10^(-4) \\ \Rightarrow x-3=0.0001 \\ add\text{ 3 to both sides of the equation} \\ x-3+3=0.0001+3 \\ \Rightarrow x=3.0001 \end{gathered}]()
Hence, the x-intercept of the function is
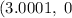
Vertical asymptote:
The vertical asymptote of the logarithm function in the form
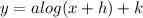
will have its vertical asymptote at
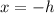
Thus, the vertical asymptote of the logarithm function:
![f(x)=\operatorname{\log}(x-3)+4]()
is
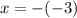
Hence, the vertical asymptote of the f(x) function is
