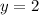Assuming that the given line is:
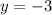
By comparing with the standard equation of a line with slope m and y-intercept equal to b:

We can see that the slope is equal to 0, and the y-intercept is equal to -3.
A line parallel to y=-3 will also have a slope equal to 0.
If the point (5,2) is in the line, then the line that we are searching for has a y-intercept of 2:
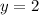
Observe that when x=5, y=2. So, the point (5,2) is that line.
Therefore, the equation of the line parallel to y=-3 that passes through the point (5,2), is: