Initial price: $10.50
final price: $10.50-$3.00 = $7.50
pieces sold: 84
final income: $699
If we establish that 'x' represents the number of items sold at the initial price and that 'y' represents the number of items sold with the final price, we can write the following equations:
equation 1.
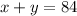
equation 2.
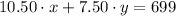
Now, we have a system of 2 equations with 2 unknowns. We can solve the system as it follows:

We obtain that 'y' is equal to 61, which indicates that 61 items were sold with the final or reduced price.
Now let's find the value of x

We obtained that 'x' equals to 23. Which means that 23 items were sold at the original price.
In conclusion:
23 -> items sold at original price
61 -> items sold at reduced price