From the given problem, it states that the distance is proportional to the body length.
So we can state that,

Where d is the distance, L is the body length and k is some constant.
The first frog has a body length of L = 2.3 in and can jump d = 119.6 in.
Solving for the value of k :
119.6=2.3(k)
k=52
We can conclude that the jumping distance of a frog is given by :
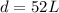
Now, find the distance of the second frog with body length of L = 2.8 in
d=52(2.8)
d=145.6 in
The answer is 145.6 in