We are given the system of equations;
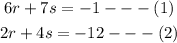
To solve a system of equations by the substitution method, we need to check and ensure that at least one of the variables has a coefficient of 1. This way it is easier to substitute the value of that variable into the other equation. For example, where we have;
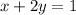
Note that x has a coefficient of 1. Therefore we can now re-write this as;
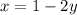
We simply take x as (1 - 2y) and substitute this wherever we see x in the other equation.
Now for the equations given we can reduce the second one by dividing all through by 2