Question

a substance has a half-life of 40 minutes. If the substance starts with 400g, how long until there is only 2g left of the substance? (round to the nearest hundredth of a minute)

Answer 1

Given:

half life of substance = 40 minutes

If the substance starts with 400g ang only 2g is left.

To find the time elapsed we have:

`\text{Elapsed time = }halflife*\frac{\log (\frac{start\text{ amount}}{end\text{ amount}})}{\log 2}`

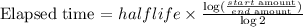
Thus, we have:

`\begin{gathered} \text{Elapsed time = 40 }*(log((400)/(2))/\log 2) \\ \\ \text{ = 40 }*\text{ }(\log 200)/(\log 2) \end{gathered}`

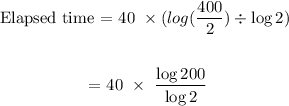
Solving further:

`40*7.64\text{ = }305.75`

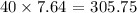
Therefore, the time elapsed until there is only 2g left is 305.75 minutes

ANSWER:

305.75 minutes