Question

If RS = 102, ST = 96, RT = 80, VW = 24, and UW = 20, find theperimeter of AUVW. Round your answer to the nearest tenth if necessary.Figures are not necessarily drawn to scale.solVwgetR

Answer 1

Two triangles are similar if the ratios of the corresponding sides are equal.

If ΔRST is similar to ΔUVW, we have that:

`(RS)/(UV)=(ST)/(VW)=(RT)/(UW)`

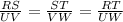
We are given the following parameters:

`\begin{gathered} RS=102 \\ ST=96 \\ RT=80 \\ VW=24 \\ UW=20 \end{gathered}`

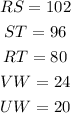
Thus, we have that:

`(102)/(UV)=(96)/(24)=(80)/(20)`

Comparing the first two ratios, we have:

`\begin{gathered} (102)/(UV)=(96)/(24) \\ (102)/(UV)=4 \\ UV=(102)/(4) \\ UV=25.5 \end{gathered}`

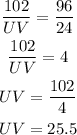
Hence, the perimeter of ΔUVW is calculated to be:

`P=UV+VW+UW=25.5+24+20=69.5`

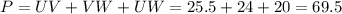
The perimeter is 69.5.