Two triangles are similar if the ratios of the corresponding sides are equal.
If ΔRST is similar to ΔUVW, we have that:
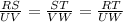
We are given the following parameters:
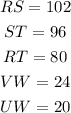
Thus, we have that:
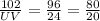
Comparing the first two ratios, we have:
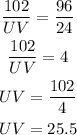
Hence, the perimeter of ΔUVW is calculated to be:
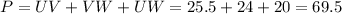
The perimeter is 69.5.