ANSWER:
a) two-term quadratic polynomial

b) three-term quadratic polynomial
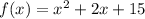
Explanation:
a) two-term quadratic polynomial

Here factoring is impossible because, then f(x) = 0:

Factoring is only possible when the polynomials have real roots.
Since value of x is imaginary, factoring is impossible
b) three-term quadratic polynomial
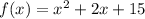
Here also when f(x) = 0
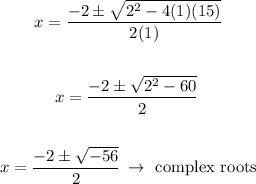
Therefore, factoring in this case is also not possible.