Question

Linear equations: solve for y, find the slop and x and y intercepts.5x - 3y = 15

Answer 1

Given the linear equation below

`5x-3y=15`

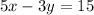
To determine the slope and the x and y intercepts

Solution:

Make y the subject of the linear equation

`\begin{gathered} 5x-3y=15 \\ 5x=15+3y \\ 15+3y=5x \\ 3y=5x-15 \\ \text{divide through by 3} \\ (3y)/(3)=(5x)/(3)-(15)/(3) \\ y=(5)/(3)x-5 \end{gathered}`

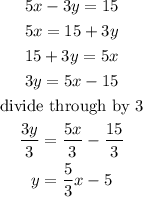
Making y the subject of the linear equation gives the slope-intercept form of a linear equation

The slope-intercept form of a linear equation is

`\begin{gathered} y=mx+c \\ m=\text{slope} \\ c=\text{intercept on the y-axis} \end{gathered}`

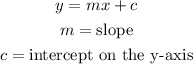
Let us compare:

`\begin{gathered} y=(5)/(3)x-5 \\ y=mx+c \\ \text{slope}=m=(5)/(3) \\ y-\text{intercept}=c=-5 \end{gathered}`

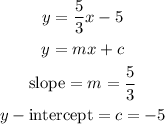
To get the x-intercept, make y = 0

`\begin{gathered} y=(5)/(3)x-5 \\ 0=(5)/(3)x-5 \\ 0+5=(5)/(3)x \\ 5=(5)/(3)x \\ 5x=3*5 \\ 5x=15 \\ x=(15)/(5) \\ x=3 \end{gathered}`

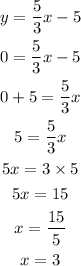
Hence,

The equation of the line in slope-intercept form is y = 5/3x - 5

Slope = 5/3

y-intercept is (0,-5)

x-intercept is (3,0)