Question

Analyze the equations in the graphs to find the slope of each equation the y-intercept of each equation in the solution for the system of equations. The slope of y = 50x + 122 is ?The slope of y = 1,540-82x is ?The y-intercept of y=50x + 122 is?The y-intercept of y = 1540-82x is? Rounded to the nearest whole number, the solution system is?

Answer 1

Writing a linear equation in the form:

`y=sx+b`

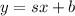
Means that "s" is the slope and "b" is the y-intercept.

So, the first one:

`\begin{gathered} y=50x+122 \\ s=50 \\ b=122 \end{gathered}`

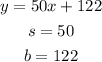
The slope is 50 and the y-intercept is 122

In the second:

`\begin{gathered} y=1,540-82x \\ y=-82x+1,540 \\ s=-82 \\ b=1,540 \end{gathered}`

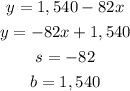
The slope is -82 and the y-intercept is 1,540.

To find the solution, both equations are solved for y, and since the solution has y = y, we have:

`\begin{gathered} 50x+122=-82x+1540 \\ 50x+82x=1540-122 \\ 132x=1418 \\ x=(1418)/(132)=(709)/(66)=10.742424\ldots\approx11 \end{gathered}`

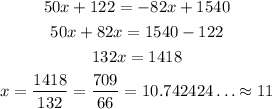
And, the y value is:

`\begin{gathered} y=50x+122 \\ y=50\cdot(709)/(66)+122 \\ y=(17725)/(33)+122=659.121212\ldots\approx659 \end{gathered}`

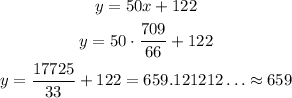
So:

The slope of y = 50x + 122 is 50

The slope of y = 1,540-82x is -82



The y-intercept of y=50x + 122 is 122

The y-intercept of y = 1540-82x is 1,540

The solution is approximately (11,659).