Question

If four postal clerks require 60 minutes to sort 1,200 letters, how many letters can 10 clerks sort in 8 hours?

Answer 1

24,000 letters.

Step-by-step explanation:

In 60 minutes, 4 postal clerks sort 1,200 letters.

`\begin{gathered} 4\text{ clerks sort 1200 letters} \\ \implies1\text{ clerk sorts }\frac{\text{1200}}{4}\text{ = 300 letters per hour} \end{gathered}`

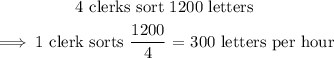
Since 1 clerk sorts 300 letters in 1 hour (i.e. 60 minutes):

`\begin{gathered} \text{In 8 hours, the number of letters sorted by 1 clerk = }(8*300) \\ \implies\text{The number of letters sorted by 10 clerks}=10*(8*300) \\ =24,000\text{ letters} \end{gathered}`

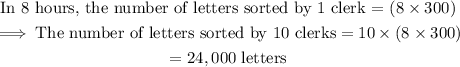
Thus, in 8 hours, 10 clerks will sort 24,000 letters.

Alternate Approach

60 minutes = 1 hour

• In 1 hour, 4 postal clerks sort 1200 letters.

,

• In 1 hour, 10 postal clerks sorts x letters.

Expressing this as a ratio:

`\begin{gathered} (1200)/(4)=(x)/(10) \\ 4x=12000 \\ x=(12000)/(4) \\ x=3,000 \end{gathered}`

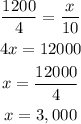
Thus, in 1 hour, 10 postal clerks will sort 3,000 letters.

Therefore, the number of letters 10 postal clerks will sort in 10 hours will be:

`\begin{gathered} 3000*8 \\ =24,000\text{ letters} \end{gathered}`

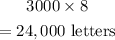
Thus, in 8 hours, 10 clerks will sort 24,000 letters.