ANSWERS
• m = ,1
,
• The point on the graph for x = 1 is (1, ,1,)
,
• Equation of the tangent at x = 1 is ,y = x
Step-by-step explanation
First, we have to find the derivative of y,
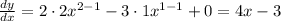
Now, to find m, we have to evaluate the derivative at x = 1,
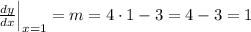
The equation of the tangent is,
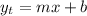
Where m is the slope - which we found above, and b is the y-intercept. To find b, we have to use a point on the line. We don't know what is the line, but we do know that it is tangent to the graph of y at the tangency point, whose x-coordinate is x = 1. To find the y-coordinate of the tangency point, we have to find y when x = 1,
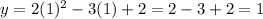
If both the graph of y and the tangent line pass through the point (1, 1), then we can use the point to find the y-intercept of the tangent line,
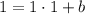
Solving for b,
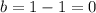
Hence, the equation of the tangent line is y = x.