Given the polynomial:
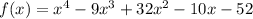
if we suppose that x = -1 is a zero of the function, when we apply sintetic division, we get:
then, our new poylinomial is:
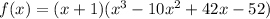
we can apply synthetic division on the second factor again if we assume that x = 2 is a zero of f(x):
so, our polynomial now looks like this:
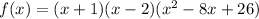
finally, using the quadratic formula on the last factor, we get:
![\begin{gathered} x=\frac{-(-8)\pm\sqrt[]{(-8)^2-4(1)(26)}}{2(1)}=\frac{8\pm\sqrt[]{64-104}}{2} \\ =\frac{8\pm\sqrt[]{-40}}{2}=(8)/(2)\pm\frac{2\sqrt[]{10}i}{2}=4\pm\sqrt[]{10}i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/2qtbf5y6xtwzjzz7ul321ghmypqhipvoyk.png)
therefore, the zeros of the function are:
![\begin{gathered} x=-1 \\ x=2 \\ x=4+\sqrt[]{10}i \\ x=4-\sqrt[]{10}i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/h4z5rnhzx8p79r7uzzwcjhqteih67ik4u2.png)