Question

The complex number Z= 1-(3 can also be written as?

Answer 1

Given the Complex Number:

`z=1-i√(3)`

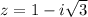
You can identify that it is written in Rectangular Form:

`z=x+yi`

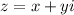
By definition, the coordinates in Rectangular Form are:

`(x,y)`

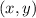
And in Polar Form:

`(r,\theta)`

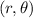
In this case, you can identify that:

`\begin{gathered} x=1 \\ y=√(3) \end{gathered}`

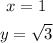
In order to convert them to Polar Form, you need to use these formulas:

`\begin{gathered} x=r\cdot cos\theta \\ y=r\cdot sin\theta \end{gathered}`

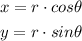
Use this formula to find "r":

`r=√(x^2+y^2)`

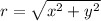
Then, this is:

`r=\sqrt{1^2+(√(3))^2}=2`

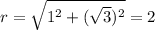
You need to find the angle. You can use this formula:

`\theta=tan^(-1)((y)/(x))`

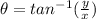
Therefore the angle is:

`\theta=tan^(-1)(-√(3))+360\text{ \degree}`

`\theta=300°`

Then:

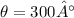
`z=2cos300\text{\degree}+2isin300\text{\degree}`

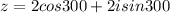
Hence, the answer is: Last option.