Let X be the normally distributed random variable representing the time hiker takes to walk the trail.
Given that mean and standard deviation are 30.1 and 3.6 minutes, respectively,

The sample size is 4,
The z-score corresponding to any value of 'x' is given by,

So the probability that the mean time for the sample is less than 28 minutes is calculated as,
![\begin{gathered} P(X<28)=P(z<(28-30.1)/(3.6)) \\ P(X<28)=P(z<-0.58) \\ P(X<28)=P(z>0.58) \\ P(X<28)=P(z>0)-P(0From the Standard Normal Distribution Table,[tex]\varnothing(0.58)=0.2190]()
Substitute the value,
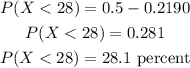
Thus, there is approximately 28.1% probability that the mean time for the sample is less than 28 minutes.