Question

For a particular nature trail, the amounts of time that hikers take to walk the trail are normally distributed.The mean of the times is 30.1 minutes,and the standard deviation is 3.6 minutes.For a sample of 4 hikers,what is the probability that the mean time for the sample is less than 28 minutes?

Answer 1

Let X be the normally distributed random variable representing the time hiker takes to walk the trail.

Given that mean and standard deviation are 30.1 and 3.6 minutes, respectively,

`\begin{gathered} \mu=30.1 \\ \sigma=3.6 \end{gathered}`

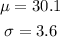
The sample size is 4,

`n=4`

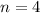
The z-score corresponding to any value of 'x' is given by,

`z=(x-\mu)/(\sigma)`

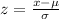
So the probability that the mean time for the sample is less than 28 minutes is calculated as,

Substitute the value,

`\begin{gathered} P(X<28)=0.5-0.2190 \\ P(X<28)=0.281 \\ P(X<28)=28.1\text{ percent} \end{gathered}`

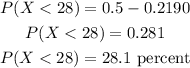
Thus, there is approximately 28.1% probability that the mean time for the sample is less than 28 minutes.