• Given Function A:
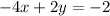
You need to remember that, by definition, the value of "y" is zero when the function intersects the x-axis.
Therefore, you need to set up that:

Substitute this value into the function and then solve for "x", in order to find the x-intercept:
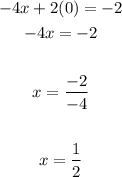
• Given that Function B passes through these points:
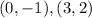
You need to determine the equation of the line, in order to find the x-intercept using it.
The Slope-Intercept Form of the equation of a line is:

Where "m" is the slope of the line and "b" is the y-intercept.
By definition, the value of "x" is zero when the function intersects the y-axis. Therefore, knowing the first point given in the exercise (whose x-coordinate is zero), you can determine that, for this line:
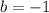
Substitute "b" and the coordinates of the second point into this equation:

And then solve for "m":
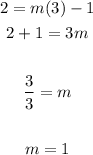
Therefore, the equation of Function B in Slope-Intercept Form is:
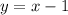
Now you can find the x-intercept by using the procedure used for Function A:
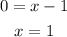
You know that:
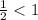
Hence, the answer is: Third option.