Question

Find the area of this triangle and the values of x and y

Answer 1

First let's find the value of x using the Pythagorean theorem in the left small triangle:

`\begin{gathered} 14^2=6^2+x^2 \\ 196=36+x^2 \\ x^2=196-36 \\ x^2=160 \\ x=\sqrt[]{160}=4\sqrt[]{10}=12.65 \end{gathered}`

Now, finding the value of y with the Pythagorean theorem in the right small triangle, we have:

`\begin{gathered} 16^2=x^2+y^2 \\ 256=160+y^2 \\ y^2=256-160 \\ y^2=96 \\ y=\sqrt[]{96}=4\sqrt[]{6}=9.8 \end{gathered}`

The area of the triangle is calculated with the formula:

`\text{area}=(b\cdot h)/(2)`

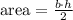
Where b is the base and h is the height relative to this base. Using b = 6 + y and h = x, we have:

`\begin{gathered} \text{area}=((6+y)x)/(2) \\ \text{area}=\frac{(6+4\sqrt[]{6})4\sqrt[]{10}}{2} \\ \text{area}=(6+4\sqrt[]{6})2\sqrt[]{10} \\ \text{area}=12\sqrt[]{10}+8\sqrt[]{60} \\ \text{area}=12\sqrt[]{10}+16\sqrt[]{15} \\ \text{area}=12\cdot3.162+16\cdot3.873 \\ \text{area}=99.912 \end{gathered}`