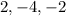SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given polynomial function
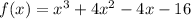
STEP 2: Apply the factor theorem
A polynomial function f(x) has a factor (x-a) if and only if f(a) = 0, this means that (x-2) will be a factor if and only if f(2)=0.
By checking,
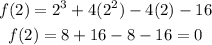
Hence, (x-2) is a factor and the first zero is 2
STEP 3: We divide the polynomial by its factor to get the quotient expression
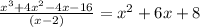
STEP 4: we find out the factors of the quotient
If f(a) is zero, this means that a must be a factor of 16
The factors of 16 are 1,2,4,8,16
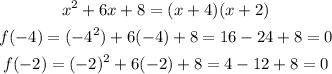
Hence, (x+4) and (x+2) are also factors of the polynomial.
Therefore, the zeroes of the given function are: