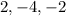Question

Use the Factor Theorem to find the zeros of f(x) = x³+4x² - 4x - 16 given that (x - 2) is afactor of the polynomial.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given polynomial function

`f(x)=x^3+4x^2-4x-16`

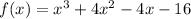
STEP 2: Apply the factor theorem

A polynomial function f(x) has a factor (x-a) if and only if f(a) = 0, this means that (x-2) will be a factor if and only if f(2)=0.

By checking,

`\begin{gathered} f(2)=2^3+4(2^2)-4(2)-16 \\ f(2)=8+16-8-16=0 \end{gathered}`

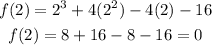
Hence, (x-2) is a factor and the first zero is 2

STEP 3: We divide the polynomial by its factor to get the quotient expression

`(x^3+4x^2-4x-16)/((x-2))=x^2+6x+8`

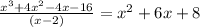
STEP 4: we find out the factors of the quotient

If f(a) is zero, this means that a must be a factor of 16

The factors of 16 are 1,2,4,8,16

`\begin{gathered} x^2+6x+8=(x+4)(x+2) \\ f(-4)=(-4^2)+6(-4)+8=16-24+8=0 \\ f(-2)=(-2)^2+6(-2)+8=4-12+8=0 \end{gathered}`

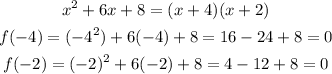
Hence, (x+4) and (x+2) are also factors of the polynomial.

Therefore, the zeroes of the given function are:

`2,-4,-2`