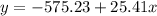The general formula for the least-squares regression is:
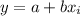
Where
a represents the y-intercept
b represents the slope
To estimate the y-intercept and the slope of the regression line you have to apply the following formulas:
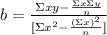
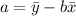
First, calculate the sums and the means for both variables.
X= screen size
Y= price
n=7
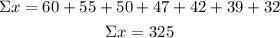
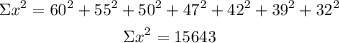
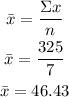
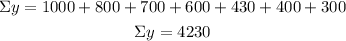
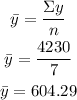
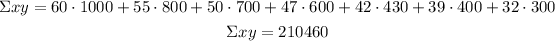
Calculate the slope of the line:
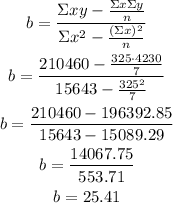
Once you have calculated the slope, you can calculate the y-intercept:
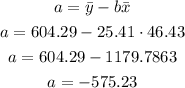
The regression line for the price with respect to the screen size is: