Question

6. The members of the boosters organization at your high school bought new sports equipment for the school.They spent $26.00 per basketball and $40.00 per football, spending a total of $860.00. They bought 5 lessbasketballs than footballs. How many of each type of ball did they buy?

Answer 1

Let number of basketball be "b", and number of football be "f".

We can write 2 equations from the statements.

"bought 5 less basketballs than footballs":

`f=b+5`

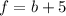
"Basketballs cost 26 and footballs cost 40 dollars each and total spent is 860 dollars":

`26b+40f=860`

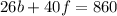
We can substitute equation 1 into equation 2 and solve for b. Shown below:

`\begin{gathered} 26b+40f=860 \\ 26b+40(b+5)=860 \\ 26b+40b+200=860 \\ 66b=860-200 \\ 66b=660 \\ b=(660)/(66) \\ b=10 \end{gathered}`

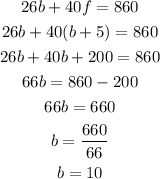
Now, we can find f:

`\begin{gathered} f=b+5 \\ f=10+5 \\ f=15 \end{gathered}`

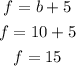
So,

10 basketballs bought and 15 footballs bought