hello
the equation of a straight line is given as
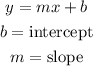
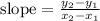
from the graph given the values of the co-ordinates are given as
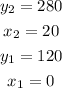
now let's substitute the values into the equation and solve
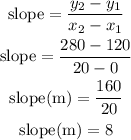
from the calculations above, the slope of the line is equal to 8 and also the y-intercept is equal to 120
the equation of the line =
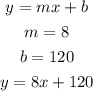
the equation of the line is y = 8x + 120 and this correspo