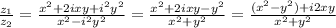Question

Explain to me what Dividing complex numbers is? and give ma an example.

Answer 1

Complex numbers comprise of two parts, namely: real and imaginary parts.

A typical complex number is given as

`z=x+iy`

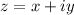
Where x is the real part and y is the imaginary part

Now, how do we perform division for complex numbers?

Given two complex numbers Z₁ and Z₂, such that

`\begin{gathered} z_1=x+iy \\ z_2=x-iy \\ \end{gathered}`

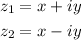
Dividing Z₁ by Z₂ gives

`\begin{gathered} (z_1)/(z_2)=(x+iy)/(x-iy) \\ \end{gathered}`

We multiply the fraction by the conjugate of the denominator. The conjugate of Z₂ (denominator) is

`x+iy`

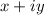
Thus, we have

`(z_1)/(z_2)=(x+iy)/(x-iy)*(x+iy)/(x+iy)=((x+iy)(x+iy))/((x-iy)(x+iy))=((x^2+ixy+ixy+i^2y^2))/(x^2-ixy+ixy-i^2y^2)`

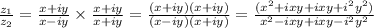
Collecting like terms, we have

`(x^2+2ixy+i^2y^2)/(x^2-i^2y^2)`

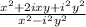
But i²= -1. Thus,

`(z_1)/(z_2)=(x^2+2ixy+i^2y^2)/(x^2-i^2y^2)=(x^2+2ixy-y^2)/(x^2+y^2)=((x^2-y^2)+i2xy)/(x^2+y^2)`