We will have the following:
1st:
* Determinant:
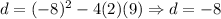
* #x-intecepts: GIven the determinant we can see that there are no x-intercepts.
2nd:
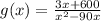
*Verical Asymptotes:
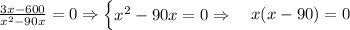
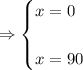
So, there are two vertical asymptotes at x = 0 & x = 90.
*Horizontal Asymptotes:
We can see that the degree of the denominator is greater than that of the numerator so, there is a horizontal asymptote at y = 0.
*x-Intercept:
Since there is a horizontal asymptote at y = 0 and the function becomes undefined when x = 0, there is no x-intercept in this function. [Being very technical it could be stated that there are x-intercepts at (-∞, 0) & (∞, 0), but since these vales are undefined they are of little use]