Question

Use the laws of exponents to solve the following exponential equation.(x - 2)^1/2 = 9^1/4

Answer 1

To solve this question we will use the following properties of exponents:

`\begin{gathered} (a^(2m))^{(1)/(2m)}=|a|. \\ (a^{(1)/(m)})^m=a. \\ (a^m)^n=a^(mn.) \end{gathered}`

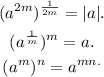
Now, notice that:

`\begin{gathered} 9=3^2, \\ (1)/(4)=(1)/(2)\cdot(1)/(2)\text{.} \end{gathered}`

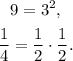
Therefore:

`\begin{gathered} 9^{(1)/(4)}=9^{(1)/(2)\cdot(1)/(2)}=(9^{(1)/(2)})^{(1)/(2)} \\ =((3^2)^{(1)/(2)})^{(1)/(2)}=3^{(1)/(2)}. \end{gathered}`

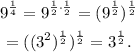
Substituting the above result in the given equation we get:

`(x-2)^{(1)/(2)}=3^{(1)/(2)}.`

Taking the above equation to the power of 2 we get:

`\begin{gathered} ((x-2)^{(1)/(2)})^2=(3^{(1)/(2)})^2, \\ x-2=3. \end{gathered}`

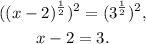
Adding 2 to the above equation we get:

`\begin{gathered} x-2+2=3+2, \\ x=5. \end{gathered}`

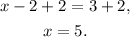
Answer: Option b.