Given the word problem, we can deduce the following information:
1. We use a 95% degree of confidence.
2. n=2000, x=300
To find the Margin of Error, we use the formula:
![ME=z\cdot\sqrt[]{(p(1-p))/(n)}](https://img.qammunity.org/2023/formulas/mathematics/college/qejpy39q6cr05o6xvbmg71ldn68szv2dou.png)
where:
ME= Margin of Error
p=sample proportion
n=sample size
z=z-value
We can get the sample proportion, p by using the formula:
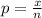
where:
x=number of successes
So,
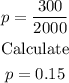
Since the degree of confidence is 95%, the z-value is 1.96 or z=1.96.
Next, we plug in z=1.96, p=0.15, and n=2000 into the Margin of Error formula:
![\begin{gathered} ME=z\cdot\sqrt[]{(p(1-p))/(n)} \\ =(1.96)(\sqrt[]{(0.15(1-0.15))/(2000)} \\ \text{Calculate} \\ ME=0.0156 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dmsaa0w9fcv2bi7a9nxcswtabt3oblldsk.png)
Therefore, the Margin of Error is 0.0156.