Given:
The objective is to prove that each pair of consecutive angles of a parallelogram are supplementary angles.
Step-by-step explanation:
Consider a parallelogram ABCD with opposite parallel sides.
First consider the parallel sides AB || CD. Then, the sides AD and BC are transversal lines.
By the property of parallel lines, the sum of the angles on same side of a transversal is 180°.
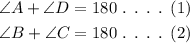
Now, consider the parallel sides as AD || BC. Then, the sides AB and CD are transversal lines.
By the property of parallel lines, the sum of the angles on same side of a transversal is 180°.

Thus, the sum of any two sides of a parallelogram will always be 180°.
Hence, it is proved that in a parallelogram each pair of consecutive angles are supplementary.