We have
vi=initial velocity=10.2 m/s
θ=25°
a)
We have that for
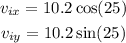
Then for
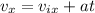
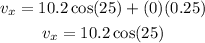
For vy
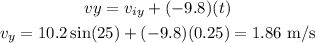
For the magnitude of the velocity
![v=\sqrt[]{(10.2\cos 25)^2+1.86^6}=9.43\text{ m/s}](https://img.qammunity.org/2023/formulas/physics/college/6qyww1r32wdbqajis3hnj9ui4psk6cda21.png)
For the direction of the velocity
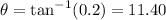
For part b)
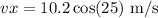
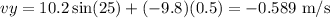
For the magnitudeof the velocity
![v=\sqrt[]{(10.2\cos (25))^2+(-0.589)^2}=9.26\text{ m/s}](https://img.qammunity.org/2023/formulas/physics/college/546zec6jdjerdifbpgdjvc0tbrsl9hu0ap.png)
For the direction of the velocity
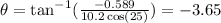
For c)
Because of the negative sign that we obtain in the velocity, we can say that the greatest height is located before the 0.5 m