Question

50. A soccer ball is kicked with an initial speed of 10.2 m/s in a direction 25.0° above the horizontal. Find the magnitude and direction of its velocity (a) 0.250 s (b) 0.500 s after being kicked. (c) Is the ball at its greatest height before or after 0.500 s? Explain.

Answer 1

We have

vi=initial velocity=10.2 m/s

θ=25°

a)

We have that for

`\begin{gathered} v_(ix)=10.2\cos (25) \\ v_(iy)=10.2\sin (25) \end{gathered}`

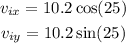
Then for

`v_x=v_(ix)+at`
`\begin{gathered} v_x=10.2\cos (25)+(0)(0.25) \\ v_x=10.2\cos (25) \end{gathered}`

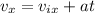
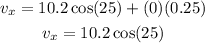
For vy

`\begin{gathered} vy=v_(iy)+(-9.8)(t) \\ v_y=10.2\sin (25)+(-9.8)(0.25)=1.86\text{ m/s} \end{gathered}`

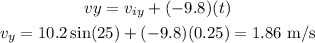
For the magnitude of the velocity

`v=\sqrt[]{(10.2\cos 25)^2+1.86^6}=9.43\text{ m/s}`

For the direction of the velocity

`\theta=\tan ^(-1)(0.2)=11.40\text{ \degree}`

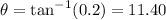
For part b)

`vx=10.2\cos (25)\text{ m/s}`

`vy=10.2\sin (25)+(-9.8)(0.5)=-0.589\text{ m/s}`

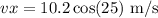
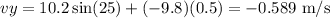
For the magnitudeof the velocity

`v=\sqrt[]{(10.2\cos (25))^2+(-0.589)^2}=9.26\text{ m/s}`

For the direction of the velocity

`\theta=\tan ^(-1)((-0.589)/(10.2\cos (25)))=-3.65\text{ \degree}`

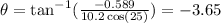
For c)

Because of the negative sign that we obtain in the velocity, we can say that the greatest height is located before the 0.5 m