We are asked to determine the sum of the two vectors F1 and F2. To do that we will use the following triangle:
Therefore, substituting the magnitudes of the vectors the triangle is:
Now, to determine the magnitude of the resultant force "R" we will use the cosine law:
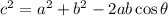
Where:
Now, we substitute the values:
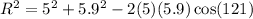
Solving the operations we get:
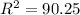
Now, we take the square root to both sides:
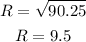
Therefore, the magnitude of the sum of vectors is 9.5
Now, we determine the angle:
We need to determine angle "y". To do that we will determine the angle "x" using the sine law:
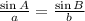
Where:
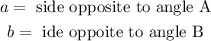
Now, we plug in the known values:
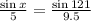
Now, we multiply both sides by 5:
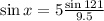
Solving the operations:
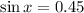
Now, we take the inverse function of the sine:
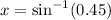
Solving the operations:
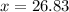
Now, we have that since F1 is a vertical force then the sum of angles "x" and "y" must add up to 90:
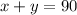
Now, we substitute the value of angle "x":
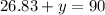
Now, we subtract 26.83 from both sides:
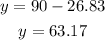
Therefore, the angle of the sum of vectors is 63.17°.