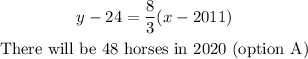Question

Nadia finds out that her favorite horse family population is increasing at a constant rate. The horse family was at 24 in 2011 and is currently at 32 in 2014. Find an equation in point slope form that models the population growth in predict the number of horses in 2020. Select the correct response:

Answer 1

`\begin{gathered} y-24=(8)/(3)(x-2011) \\ \text{There will be 48 horses in 2020 (option A)} \end{gathered}`Step-by-step explanation:

The initial number of horses = 24

year = 2011

Coordinates (2011, 24)

when the number of horses became 32, year was 2014

Coordinates (2014, 32)

We find the slope = rate of change

slope = change in number of horses/change in number of years

slope = (32-24)/(2014-2011)

slope = 8/3

The point slope formula:

`\begin{gathered} y-y_1=m(x-x_1) \\ U\sin gpoint\colon x_1=2011,y_1=24 \end{gathered}`
`y-24=(8)/(3)(x-2011)`

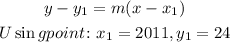
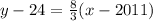
The number of horses in year 2020

using points: (2011, 24) and (2020, y), we equate with the slope since it is constant for any two points on this model.

8/3 = (y - 24)/(2020 - 2011)

8/3 = (y - 24)/9

cross multiply:

8(9) = 3(y - 24)

72 = 3y - 72

72 + 72 = 3y

144 = 3y

144/3 = 3y/3

y = 48

Hence, there will be 48horses in 2020 (option A)