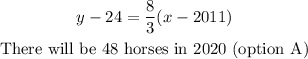 Step-by-step explanation:
Step-by-step explanation:The initial number of horses = 24
year = 2011
Coordinates (2011, 24)
when the number of horses became 32, year was 2014
Coordinates (2014, 32)
We find the slope = rate of change
slope = change in number of horses/change in number of years
slope = (32-24)/(2014-2011)
slope = 8/3
The point slope formula:
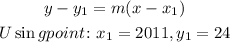
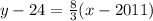
The number of horses in year 2020
using points: (2011, 24) and (2020, y), we equate with the slope since it is constant for any two points on this model.
8/3 = (y - 24)/(2020 - 2011)
8/3 = (y - 24)/9
cross multiply:
8(9) = 3(y - 24)
72 = 3y - 72
72 + 72 = 3y
144 = 3y
144/3 = 3y/3
y = 48
Hence, there will be 48horses in 2020 (option A)