ANSWER
The average rate of change of the function is 3
Explanation
Given the below function

The formula for calculating the average rate of change is written below as
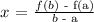
Where (a, b) is the interval of the function
let a = - 1 and b = 1
The next thing is to substitute the value of a and b into the function to find the value of the function.
for a = -1
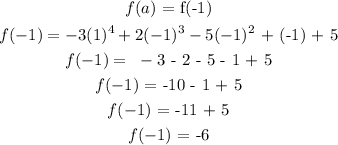
Find the value of the function when b = 1
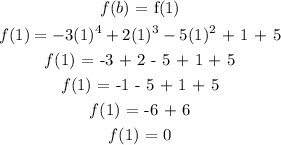
recall that, the average rate formula is given below as
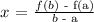
Substitute the value of f(a) and f(b) into the formula

Hence, the average rate of change for the function is 3