Question

Calculate the average rate of change for the function f(x) = - 3x ^ 4 + 2x ^ 3 - 5x ^ 2 + x + 5 from x = - 1 to x = 1

Answer 1

The average rate of change of the function is 3

Explanation

Given the below function

`f(x)=-3x^4+2x^3-5x^2\text{ + x + 5}`

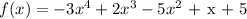
The formula for calculating the average rate of change is written below as

`x\text{ = }\frac{f(b)\text{ - f(a)}}{b\text{ - a}}`

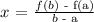
Where (a, b) is the interval of the function

let a = - 1 and b = 1

The next thing is to substitute the value of a and b into the function to find the value of the function.

for a = -1

`\begin{gathered} f(a)\text{ = f(-1)} \\ f(-1)=-3(1)^4+2(-1)^3-5(-1)^2\text{ + (-1) + 5} \\ f(-1)=\text{ }-3\text{ - 2 - 5 - 1 + 5} \\ f(-1)\text{ = -10 - 1 + 5} \\ f(-1)\text{ = -11 + 5} \\ f(-1)\text{ = -6} \end{gathered}`

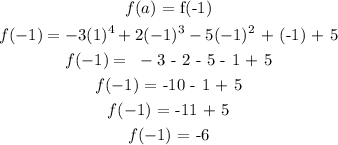
Find the value of the function when b = 1

`\begin{gathered} f(b)\text{ = f(1)} \\ f(1)=-3(1)^4+2(1)^3-5(1)^2\text{ + 1 + 5} \\ f(1)\text{ = -3 + 2 - 5 + 1 + 5} \\ f(1)\text{ = -1 - 5 + 1 + 5} \\ f(1)\text{ = -6 + 6} \\ f(1)\text{ = 0} \end{gathered}`

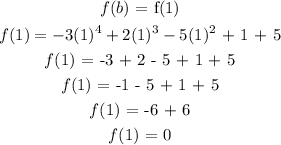
recall that, the average rate formula is given below as

`x\text{ = }\frac{f(b)\text{ - f(a)}}{b\text{ - a}}`

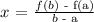
Substitute the value of f(a) and f(b) into the formula

`\begin{gathered} x\text{ = }\frac{0\text{ - (-6)}}{1\text{ - (-1)}} \\ x\text{ = }\frac{0\text{ + 6}}{1\text{ + 1}} \\ x\text{ = }(6)/(2) \\ x\text{ = 3} \end{gathered}`

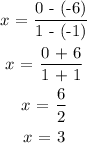
Hence, the average rate of change for the function is 3