Question

A car's bumper is designed to withstand a 6.48-km/h (1.8-m/s) collision with an immovable object without damage to the body of the car. The bumper cushions the shock by absorbing the force over a distance. Calculate the magnitude of the average force on a bumper that collapses 0.210 m while bringing a 830-kg car to rest from an initial speed of 1.8 m/s.

Answer 1

6402.86 N

Step-by-step explanation:

taking into account the energy-work theorem, we can write the following equation

`\begin{gathered} W=K_f-K_i \\ Fd=(1)/(2)mv_f^2-(1)/(2)mv_i^2 \end{gathered}`

Where F is the force, d is the distance, m is the mass, vf is the final velocity and vi is the initial velocity.

Solving for F, we get:

`F=(mv_f^2-mv_i^2)/(2d)`

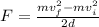
Replacing m = 830 kg, vf = 0 m/s, vi = 1.8 m/s, and d = 0.210 m, we get:

`F=((830)(0)^2-(830)(1.8)^2)/(2(0.210))=-6402.86\text{ N}`

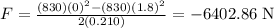
Therefore, the magnitude of the force is 6402.86 N