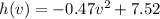Question

h is a quadratic function where h(4) = 0, h( - 4) = 0, and h(0) = 7.52. Find an algebraic equation forh(v)

Answer 1

The first thing we have to know is that a quadratic equation is given by the following equation:

`h(v)=Av^2+Bv+C`

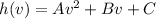
Where A, B and C with constants.

The exercise gives us 3 points and with those 3 points we are going to calculate the values for A, B and C and thus be able to find the equation h (v)

`\begin{gathered} h(0)=7.52 \\ 7.52=A(0^2)+B(0)+C \\ C=7.52 \end{gathered}`

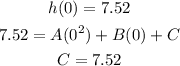
Now the value of C can be replaced in the equation

`\begin{gathered} h(4)=0 \\ 0=A(4)^2+B(4)+7.52 \\ 16A+4B+7.52=0 \\ 16A=-4B-7.52 \end{gathered}`
`\begin{gathered} h(-4)=0 \\ 0=A(-4)^2+B(-4)+7.52 \\ 16A-4B+7.52=0 \\ 16A=4B-7.52 \end{gathered}`

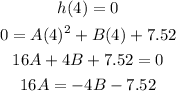
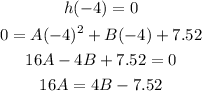
In the 2 equations that we have left, it has the common factor 16A so we are going to equal it to calculate B

`\begin{gathered} -4B-7.52=4B-7.52 \\ 8B=-7.52+7.52 \\ 8B=0 \\ B=0 \end{gathered}`

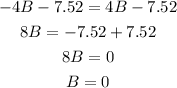
Replacing B to find A:

`\begin{gathered} 16A=4(0)-7.52 \\ A=(-7.52)/(16) \\ A=-0.47 \end{gathered}`

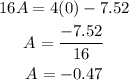
The values of A, B and C are replaced in the equation of the general quadratic function

`h(v)=-0.47v^2+7.52`