Question

A motorboat travels 275 kilometers in 5 hours going upstream and 372 kilometers in 4 hours going downstream. What is the rate of the boat in still water and what is the rate of the current?

Answer 1

We are given that a boat travels upstream a distance of 275 kilometers in 5 hours. This is the speed of the boat when it goes against the current of the river, therefore, we have:

Where:

`\begin{gathered} v_b=\text{ rate of the boat} \\ v_r=\text{ rate of the river} \end{gathered}`

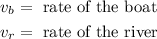
Simplifying we get:

Now, when the boat travels downstream then the relative speed of the boat is determined by adding both velocities, therefore, we have:

Simplifying we get:

Now we have two equations and two variables. To solve the system we can add both equations and we get:

Adding like terms:

Now we divide both sides by 2:

Therefore, the rate of the boat is 74 km/h. To determine the rate of the river we substitute this rate in the first equation:

Now we solve for the rate of the rive first by subtracting 74 from both sides:

Solving the operations:

Now we multiply both sides by -1:

Therefore, the rate of the river is 19 km/h.