1 Answer

Amadou Beye · Answer 1 · 2024-01-04T03:05:54+0000

Given:

The length of the rectangular desktop in scale drawing, l=4 cm.

The width of the rectangular desktop in scale drawing, w=1.5 cm.

The width of the actual desktop, W=1.2 m.

The scale factor for obatining the original dimensions of the desktop is,

$S=(W)/(w)=\frac{1.2\text{ m}}{1.5\operatorname{cm}}=\frac{1.2*10^2\text{ cm}}{1.5\text{cm}}=(4*10^2)/(5)=80$

Multiply the length l of the rectangular desktop in scale drawing by the scale factor S to get the length of the actual desktop.

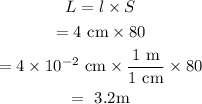
$\begin{gathered} L=l* S \\ =4\text{ cm}*80 \\ =4*10^(-2)\text{ cm}*\frac{1\text{ m}}{1\text{ cm}}*80 \\ =\text{ 3.2m} \end{gathered}$

Now, the actual area of the desktop is,

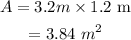
$\begin{gathered} A=3.2m*1.2\text{ m} \\ =3.84\text{ }m^2 \end{gathered}$

Therefore, the actual area of the desktop is 3.84 sq m.

Please log in or register to add a comment.