Given:
The length of the rectangular desktop in scale drawing, l=4 cm.
The width of the rectangular desktop in scale drawing, w=1.5 cm.
The width of the actual desktop, W=1.2 m.
The scale factor for obatining the original dimensions of the desktop is,
![S=(W)/(w)=\frac{1.2\text{ m}}{1.5\operatorname{cm}}=\frac{1.2*10^2\text{ cm}}{1.5\text{cm}}=(4*10^2)/(5)=80]()
Multiply the length l of the rectangular desktop in scale drawing by the scale factor S to get the length of the actual desktop.
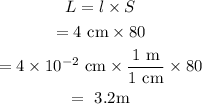
Now, the actual area of the desktop is,
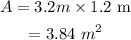
Therefore, the actual area of the desktop is 3.84 sq m.