Question

What's the equation of a circle whose endpoints of its diameter are (2,6) and (8,-6).

Answer 1

The general form of an equation is given by

`(x-a)^2+(x-b)^2=r^2`

where (a,b) are the coordinates of the centre and r is the radius of the circle.

Now the coordinates of the centre are the midpoint of the points (2,6) and (8,-6). ​

The midpoint is calculated as follows

The vertical distance between (2,6) and (8,-6) is

`6-(-6)=12`

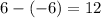
half of this is 6.

The horizontal distance between (2,6) and (8,-6) is

`2-8=-6`

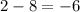
half of which is -3.

suntracting y = 6 and x = -3 to (2,6) gives

`(2+3,6-6,)=(5,0)`

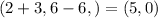
Hence, the coordinates of the centre are (a, b ) (5,0).

Now, the radius of the circle is half the distance to the midpoint

`\begin{gathered} r=\sqrt[]{6^2+(-3)^3} \\ r=3\sqrt[]{5} \end{gathered}`

Hence, the equation for the circle is

`\begin{gathered} (x-5)^2+y^2=(3\sqrt[]{45}) \\ (x-5)^2+y^2=45 \end{gathered}`