The equation of the given parabola is

Rewrite the equation in the vertex form

The equation becomes
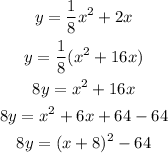
Divide through the equation by 8
This gives
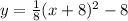
Comparing the equation with the vertex form
It follows
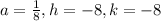
The focus of a parabola in vertex form is given as
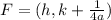
Substitute h = -8, k = -8 and a = 1/8 into the formula for focus
This gives
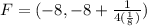
Simplify the expression
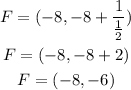
Therefore, the focus of the parabola is at (-8, -6)