Question

The length of a rectangle is 4 inches shorter than twice the width (x),Which is the area (y) when the width (x) is 16 inches?

Answer 1

The area of a rectangle can be found with this formula:

`A=lw`

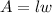
Where "l" is the length and "w" is the width.

In this case, let be "x" the width of the rectangle (in inches) and "y" the area of the rectangle (in square inches). So you can rewrite the formula as:

`y=lx`

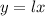
Knowing that its length is 4 inches shorter than twice the width, you can write this equation:

`l=2x-4`

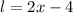
Substitute this equation into the previous one:

`\begin{gathered} y=(2x-4)x \\ y=2x^2-4x \end{gathered}`

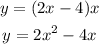
To calculate the area of the rectangle when the width is 16 inches, you must substitute this value into the last equation and evaluate. This is:

`\begin{gathered} y=2(16)^2-4(16) \\ y=512-64 \\ y=448 \end{gathered}`

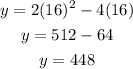
The answer is : LAST OPTION.