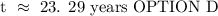SOLUTION:
Step 1:
In this question, we are given the following:
The half-life of Pb-210 is 22 years.
A decayed animal shows 48% of the original Pb-210 remains;
how long has the animal been deceased to the nearest tenth of a year?
Step 2:
The details of the solution are as follows:
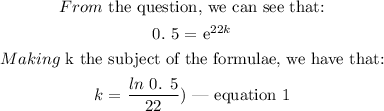
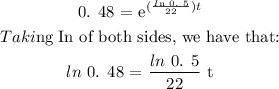
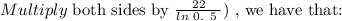
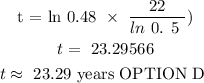
CONCLUSION:
The final answer is: