Question

A recent high school graduate received $800 in gifts of cash from friends and relatives. In addition, he received three scholarships in the amounts of $450, $600, $1300. If he takes all his gifts and scholarship money and invests it in a 36-month CD paying 4% interest compound daily, how much will the graduate have when he cashes in the CD at the end of the 36-months?

Answer 1

Given:

a.) A recent high school graduate received $800 in gifts of cash from friends and relatives.

b.) In addition, he received three scholarships in the amounts of $450, $600, $1300.

We will be using the Compound Interest Formula:

`\text{ A = P(1 + }(r)/(n))^(nt)`

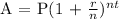
Where,

A = accumulation (the amount of money accumulated after n years with interest)

P = principal (the initial amount you borrow or invest)

r = annual interest rate (in decimal)

n = the number of times the interest is compounded per year

t = the number of years the amount is borrowed or invested for

P = gifts + scholarships = 800 + 450 + 600 + 1300 = $3,150

r = 4% = 4/100 = 0.04

n = daily = 365

t = 36 months = 36/12 = 3 years

We get,

`\text{ A = P(1 + }(r)/(n))^(nt)`
`\text{ = (3,150)(1 + }(0.04)/(365))^((365)(3))`
`\text{ = (3,150)(}1\text{ + }0.00010958904)^(1,095)`
`\text{ = (3,150)(}1.00010958904)^(1,095)`
`\text{ = (3,150)(}1.12748943847)`
`\text{ = }3,551.59173117`
`\text{ A }\approx\text{ \$}3,551.59`

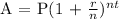
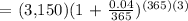
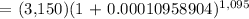
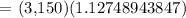
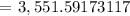
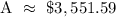
Therefore, the answer is $3,551.59