Given:
a.) A recent high school graduate received $800 in gifts of cash from friends and relatives.
b.) In addition, he received three scholarships in the amounts of $450, $600, $1300.
We will be using the Compound Interest Formula:
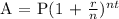
Where,
A = accumulation (the amount of money accumulated after n years with interest)
P = principal (the initial amount you borrow or invest)
r = annual interest rate (in decimal)
n = the number of times the interest is compounded per year
t = the number of years the amount is borrowed or invested for
P = gifts + scholarships = 800 + 450 + 600 + 1300 = $3,150
r = 4% = 4/100 = 0.04
n = daily = 365
t = 36 months = 36/12 = 3 years
We get,
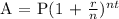
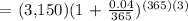
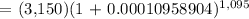
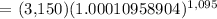
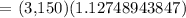
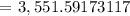
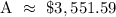
Therefore, the answer is $3,551.59