The question talks about two quadrilaterals GHJK and CVBN that are similar.
The area of GHJK = 250 square feet
The area of CVBN = 10 square feet.
We are given the perimeter of GHJK and asked to find perimeter of CVBN.
In order to solve this problem, we will follow these steps:
1. Find the ratio of the areas of the two quadrilaterals.
2. The ratio of the areas of two similar shapes is equal to the square of the lengths of the shapes.
As a result, the ration of the areas is equal to the square of the perimeters of the shapes. Thus, find the square root of the ratio.
3. Equate the square root of the ratio from step 2 to the ratio of the perimeters of the two shapes.
With these steps, let us solve the question.
1. Find the ratio of the areas of the two quadrilaterals.
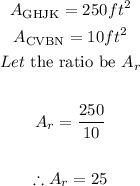
2. Find the square root of the ratio
![\begin{gathered} A_r=25 \\ \text{ Find the square root of the ratio of the areas} \\ \sqrt[]{A_r}=\sqrt[]{25} \\ \sqrt[]{A_r}=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8g6h7r5hacjidcwjzz6gbuvegi34uq3rg3.png)
3. Equate the square root of the ratio from step 2 to the ratio of the perimeters of the two shapes.
![\begin{gathered} \text{let the perimeter of CVBN be P}_(CVBN) \\ \text{ Equating the ratio of perimeters to the square root from step 2.} \\ \\ P_{\text{GHJK}}=90 \\ \sqrt[]{A_r}=\frac{P_{\text{GHJK}}}{P_{\text{CVBN}}} \\ \\ 5=\frac{90}{P_{\text{CVBN}}}\text{ (Cross - multiply)} \\ \\ \therefore P_{\text{CVBN}}=(90)/(5) \\ \\ P_{\text{CVBN}}=18ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9o341zqpe1w9yc6kmip9bllxumhkqdnh2v.png)
Therefore, the final answer is:
18 feet (Option 2)
.