Step 1. Two equations have no solutions if the lines that they represent are parallel lines:
And to be parallel lines they must have the same slope and different y-intercepts.
Step 2. The two equations that we have are:
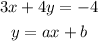
The second equation
y=ax+b
is already in the slope-intercept form where a is the slope and b is the y-intercept of the line.
The first equation
3x+4y=-4
is not in the slope-intercept form. Therefore, we solve for y:
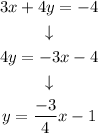
Step 3. The pair of equations now is:
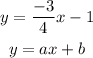
For the lines to be parallel, the slope of the two lines must be the same.
The slope of the first line is -3/4, that is the value that a should have:
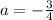
And the value of b cannot be -1 because then the equation would be the same and instead of no solutions there would be infinite solutions. Therefore a possible value can be b=1
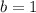
These