Step-by-step explanation:
The equation of a parabola has the following form:
f(x) = ax² + bx + c
Where a, b, and c are constant values.
If a is positive, the parabola opens up and if a is negative the parabola opens down. Additionally, the value of c is the y-intercept of the parabola, it is the point where the graph crosses the y-axis.
Therefore, if the equation of the parabola is:
f(x) = -x² + x - 5
We get that a = -1, b = 1, and c = -5
Then, since a is negative, the parabola opens down and since c is -5, the y-intercept of the parabola is -5.
Finally, the x-coordinate of the vertex of a parabola can be calculated as:
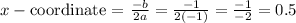
So, the y coordinate can be calculated as:
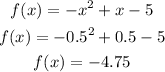
Then, the vertex of the parabola is the point (0.5, -4.75)
RT